

Before I studied physics in college, I was captivated by two of the things physicists talk about: quantum indeterminacy and curved space-time. I spent a lot of time thinking about what it might mean for a particle to be both here and there, and how something as insubstantial as space could be bent up and stitched together. Even as I learned about these things rigorously, it irked me that I couldn’t visualize them.
Eventually, I came up with ways of visualizing these things that made sense of them without doing too much violence to the underlying formalism. When I talk about curved space now, for instance, I’m imagining the contorted fabric of a pair of pants I once sewed, and how they couldn’t lay flat. I presented this explanation in a previous article on this website, but the “space-time as a sheet” metaphor is an old one that might only be helpful after a course in Riemannian geometry and another in sewing.
Computers have no trouble imagining curved spaces, and multitouch devices such as iPads let the user engage the computer’s abstractions in a palpable way. So I got to thinking, what if I write a program to directly interact with curved space? This article presents the result of that tinkering: a hyperbolic portal that runs in your browser (no need to download anything), intended to give you a direct experience of spatial curvature. The code is on GitHub, and I’d love to see (and link to) anything that you might do with it.
Stitching spaces
Every class I took to learn about curved spaces or general relativity gave me the impression that it’s a super-advanced form of calculus, with lots of “delta-epsilon” proofs. The key realization for me was that most of that complexity is just to deal with smoothness, the fact that even a simple straight line is an infinitude of infinitesimal points. It’s possible to think about curvature in a useful if mathematically imprecise way by sweeping all of the infinities under a very big rug.
Imagine that space is a grid of pixels like the dots on a computer screen. Space can contain matter in the same way that computer pixels contain color, or a part of the screen contains a button, a window, or a video game sprite. We’ll ignore the fact that pixels are not infinitely small and also the implications that would come from taking this discreteness too seriously.
All pixels, other than those along the edges of the screen, have four direct neighbors: north, west, south, and east. Suppose we make a new computer screen that has five neighbors for each pixel: replace north with two new directions, “ronth” and “ornth.” If we made all pixels the same size, then the screen couldn’t possibly be flat. It would have to curl up to have some place to put all those extra pixels. This is easier to see in knitted fabrics, since that’s exactly how one knits a curved hat— by adding a few extra stitches in each row. But on a computer screen, things can live in the curved surface.
Here is the connection between curved objects and curved spaces: the knitted hat has a shape determined by the way that equal-sized stitches are connected to each other, and a curved space is defined solely by the way that its pixels are connected to each other. The phrase “curved space” does not imply that space is somehow rounded or can be viewed as round from some place outside of it. A hat, however, needs to be inside the universe to be viewed. You could argue that the word “curvature” shouldn’t be applied to space for this reason: you could say that nineteenth century mathematicians took the concept of curvature from only one aspect of hats— the way their stitches connect— and applied it to something that has only this one aspect. It wouldn’t be an unreasonable argument. But “curvature” is just a word, and we can define words however we like. To make the distinction, mathematicians refer to the shape of an object in space as its extrinsic curvature and the pattern of stitched or pixel connections as its intrinsic curvature. Hats have both kinds; spaces may have only intrinsic curvature.
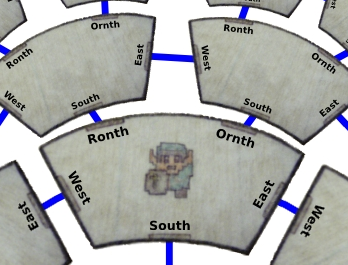
A video game character living in tiles of cloth with the logical connections between them indicated by blue lines.
The consequences of replacing north with two new directions can be hard to visualize. To see things better, let’s zoom into the pixels and make them rooms of a vast video game dungeon. The game character can go through the ronth door to get to a new room, then go east, then go south, and end up where he started. In a traditional north-west-south-east arrangement, there’s no way he could end up where he started by going through three doors. Imagine playing a game like that: your hand-drawn map would probably be full of scribbles and corrections as you come to realize that space is not what you thought it was.
Hyperbolic space
A video game with this arrangement of rooms is called a hyperbolic space. We could connect the rooms in more complicated patterns to get more complicated spaces (“warp zones” connect arbitrarily distant points in space, for instance), but let’s not. Hyperbolic, Euclidean, and spherical spaces are the three simplest ones. Euclidean is the space you know intuitively, and spherical space is like the surface of a sphere. The two-dimensional surface of the Earth could be considered a spherical space, as long as you don’t include the dirt inside and the everything else outside.


Left: the video game character’s hyperbolic world in four rows of tiles, quilted together. Right: what it would look like with infinitely many rows.
Now here’s the live version, the one you can interact with. You should see a large image below: click and drag it with the mouse, or drag it with your finger if you have a touchscreen device (iPad, smartphone, etc.).
This web application has the same kind of interactivity as Google Earth: dragging scrolls, two-finger twists rotate, the mouse-wheel and two-finger pinches zoom. Our hero lives in the room numbered zero-zero. The others are labeled by row and column, and rows are necessarily curved to fit in all the extra rooms.
The space is vast— “more infinite” in a sense than an infinite Euclidean plane. It’s easy to get lost, even with the numbered rooms. To keep your browser from overloading, the web server only sends a little data at a time, an idea borrowed from online maps. The difference here is that maps present a large spherical space, and this presents a hyperbolic one.
If you zoom all the way out, you’ll see that the whole world appears as a circular disk. This is because your computer screen is flat, and the hyperbolic plane needs to be projected to fit on it, just as a map of the world needs to project a sphere onto a flat piece of paper. I chose the Poincaré disk projection, which fits the hyper-infinite plane within a small circle. As you scroll, pictures get increasingly distorted as they approach the edge of the circle.
You may already be familiar with this projection, since it was one of M. C. Escher’s favorites. On the right is a browseable version of Circle Limit III, Escher’s woodcut of hyperbolically interlocking fishes.
Circle Limit is a uniform tiling of the hyperbolic plane, more beautiful and intricate than my ronth-west-south-east-ornth squares. In drawing this, I found that the pattern of fish is surprisingly complex: fitting them together was like trying to solve a Rubik’s cube. (I made some mistakes and gave up adding fishes a few layers from the center.) I now have a more profound respect for Mr. Escher, who not only worked out the hyperbolic projection, but designed a non-trivial tessellation symmetry and carved it in wood.
Size, distance, and straightness
Everything in the hyperbolic portal is distorted by a fish-eye lens, so objects are constantly changing their apparent sizes as they move. This artifact of the projection might hide the fact that strange things are happening to the real sizes of objects in the hyperbolic world, independent of how they are presented on your screen.
I have said that a hyperbolic plane is larger than a Euclidean plane, in spite of the fact that they’re both infinite. To be more precise, I could say that a one-inch diameter circle in hyperbolic space contains more area than a one-inch diameter circle in Euclidean space. Instead of the usual “area equals pi times radius squared” relationship (), the areas of circles in hyperbolic space grow exponentially with radius (
). Circumferences grow exponentially with radius, too.
The hyperbolic clock on the right puts this feature to use. The space is so large that it can comfortably number all of the hours, minutes, and seconds with only one hand. Try scrolling to the end of the red clock hand to reveal the minutes and the seconds.
The tick-marks and numbers labeling the minutes are all equidistant from the center of the clock, arranged to have enough space for all of the two-digit numbers— there are 12 times 60 (720) of them. The seconds are also equidistant from the center of the clock, and there are 43,200 seconds in the 12-hour cycle, individually labeled.
In our normal Euclidean clocks, we have to use special tricks to convey minutes and seconds: we need additional hands that cycle around the face of the clock more quickly than the hour hand, and we must interpret the numbers differently for those hands. This clock is simpler, though it is unfamiliar.
We could make a clock like this in Euclidean space, with one hand representing hours, minutes, and seconds, but the seconds would have to be 60 times as far from the center as the minutes, or we’d have to draw them in a very small font. (There’s 60 times as many seconds as minutes, so the circumference of their circle must be 60 times longer to show them all.) On the hyperbolic clock, the seconds are only a bit more than twice as far from the center as the minutes, and they’re quite legible with the same-sized font.
As you scroll along the hand of the clock, it appears to bend, especially if it gets off-center. That is an artifact of the projection: the clock hand is straight in hyperbolic space.
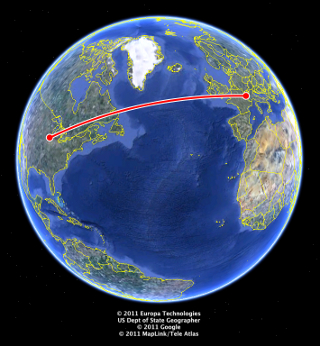
A straight line in a curved space requires a little explanation. By “straight,” I mean that it is the shortest distance between its endpoints. In a spherical space like the surface of the Earth, the shortest distance between two points is a great arc, the path that an airplane would take to get between two cities. The screenshot on the right from Google Earth shows that the shortest flight between Fermilab and CERN goes over Quebec and Ireland, which is non-intuitive on a flat map.
Curved space-time
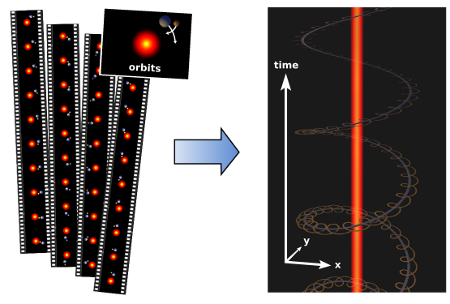
Time as a dimension: on the left is a movie of a planet orbiting a sun and a moon orbiting the planet; on the right is a space-time representation of it.
Curved spaces are strange enough, but general relativity adds one more ingredient to the mix: space-time is curved. That is, time is considered a dimension like space, and the whole four-dimensional array of space and time points is wired up like the ronth-west-south-east-ornth pixels.
The figure on the right shows how a two-dimensional moving picture can be seen as a motionless three-dimensional block of space-time. When you make time a direction, things don’t move— motion is just an angle, a direction. This is not just a matter of presentation, either. A duration of time has a physical length: one nanosecond is approximately equal to one foot (a third of a meter). Since we perceive a nanosecond as a very short time and a foot as a reasonably large distance, we have a lopsided view of space-time, making it hard to realize that we’re such long, stringy beings— only six feet high but three quintillion nanoseconds (95 years) long.
I’m committing a mathematical sin by suggesting that space and time are exactly interchangeable. There’s a minus sign in the relationship between them that affects the ways that they can be rotated, prohibiting faster-than-light travel and time travel (which are the same thing, because of this relationship). I covered this topic a little better in an article on faster-than-light neutrinos, but I’ve never found a way to describe both the effect of the minus sign and curvature in the same context, so I’ll just focus on the curvature here.
My favorite physics prop is the “space-time cone” shown below. It’s made of tiles stitched together like the hyperbolic dungeon, but now we’re interpreting one direction as altitude and the other as time. A video game character who likes to jump takes a shortcut through space-time by increasing his altitude for a little while. This shortest path, or great arc, intersects the ground at a future point— whenever you jump, curvature has the effect of putting you back on the ground, though it’s the ground that swerves to meet you, not the other way around. That’s the whole idea of general relativity, that gravity is an illusion produced by the fact that space-time is curved.

Since this is such a great demo, I made a browsable version of it. The hyperbolic portal below presents a leap through space-time that you can drag and rotate. Just like the hand of the hyperbolic clock, the jumper’s trajectory through the air is straight, but only when he’s in the air. On the ground, his trajectory is not straight, not the shortest distance between two points. That’s why gravity feels like a force: it is the ground rushing up at us, forcing us to take a rounded path through space-time, like a car turning abruptly at high speeds.
What kind of space do we live in?
Most of this article has been about math, rather than physics, because I’ve been talking about modifications to space that are conceivable, but may not be real. The space we live in appears to be Euclidean— that’s why Euclidean geometry is so intuitive. When nineteenth century mathematicians started thinking about the implications of curved spaces, Gauss attempted to measure the curvature of real space by triangulating three mountaintops in Germany. The result was consistent with zero curvature, Euclidean space.
But curvature is a relative thing: one space may be more curved than another, and curvature can be too small to measure with limited instruments. If the dungeon man were so small that he could never walk to a neighboring room, he would never know that his space is curved. If he were so large that the rooms are like pixels to him, the curvature would be very apparent. What matters is the scale of curvature compared to our scale.
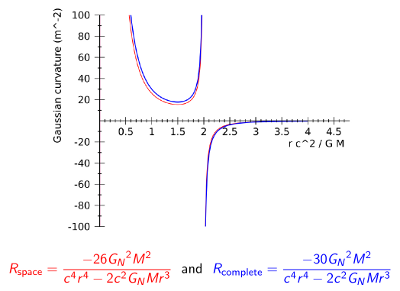
Curvature of space (red) and space-time (blue) as a function of distance from a black hole. The switch from negative curvature (hyperbolic space) to positive curvature (spherical space) is the event horizon, from whose bourn no traveler returns.
Moreover, the amount of spatial curvature may be different in different places. Real space can be hyperbolic in some places, flatten out to Euclidean in others, and be spherical in others. General relativity claims that space-time is very slightly hyperbolic near massive bodies like the Earth, and more Euclidean far from them. Close to extremely dense objects, such as black holes, the space gets very hyperbolic, then switches to spherical when you cross the point of no return.
At sea level on Earth, the curvature is −3.07×10−31 inverse meters-squared, which means that we lose 2.17×−16 meters of space (a stitch) for every meter we climb above sea level (row of stitches, knitting from the ground up). Satellites in orbit lose a microsecond every 10 minutes compared to satellite dishes on the ground, and that difference is large enough to require corrections in the electronics. The curvature of the space-time that we live in manifests itself as gravity, which we notice because we have such a foreshortened view of space-time, and in very distant, very precise electronics. It’s a hyperbolic world after all.
Hyperbolic art and software
Although I made this hyperbolic portal to demonstrate the mathematics and physics of curved spaces, it may be useful in other projects. Rather than hacking it together as a one-off demo, I developed the core functionality with readable, reusable code and put it on GitHub. The project is called hyperbolic-storage-space because of the expansive real estate that hyperbolic space provides. Wouldn’t it be cool if a file browser were rendered in hyperbolic space, so that the convenience of leaving all your files on the desktop wouldn’t make you run out of places to put them?
As I worked on it, I looked around for other projects like this one. The idea of displaying data in a hyperbolic space (in the Poincaré disk projection, no less) goes back to a 1995 demo and paper by Xerox. They even described a server-client version to put in a webpage (“subject to the glacial interaction typical of the web...”). However, all implementations that I could find, including modern ones, display only trees: words or pictures in boxes, connected by lines. Computers are now capable of rendering rich hyperbolic graphics in real time.
The GitHub repository has Javascript code for displaying vector-based graphics in a hyperbolic portal that you can pan, rotate, and zoom with a mouse or two-finger multitouch. The graphics may be a static file (in a JSON-based format) or it may be served by a Java servlet (e.g. with Tomcat). The servlet stores graphical elements in an embedded no-SQL database (BabuDB) so it can be scaled up to very large datasets, in the same way that online maps show the whole world a little at a time.
I spent some effort optimizing for speed and numerical precision. Although the images are vector-based, SVG was about ten times slower than an HTML5 canvas in several browsers, so I opted for the latter. Coordinates in the hyperbolic plane are very sensitive to numerical error due to the rapid scaling with distance that I described above. Instead of representing coordinates directly in the Poincaré disk, I found a new coordinate system in which the largest terms algebraically cancel in the transformations. I tested infinite precision arithmetic (both on the Javascript side and the Java side), but there weren’t enough gains in precision to justify the slower computations. (Square roots are involved, so an approximation needs to be made at some level.)
If you’re an artist, a programmer, or you have some neat idea that you’d like to try, take a look at the code and let me know how it goes. Merry Christmas and have a great holiday!